matedaa.blogg.se

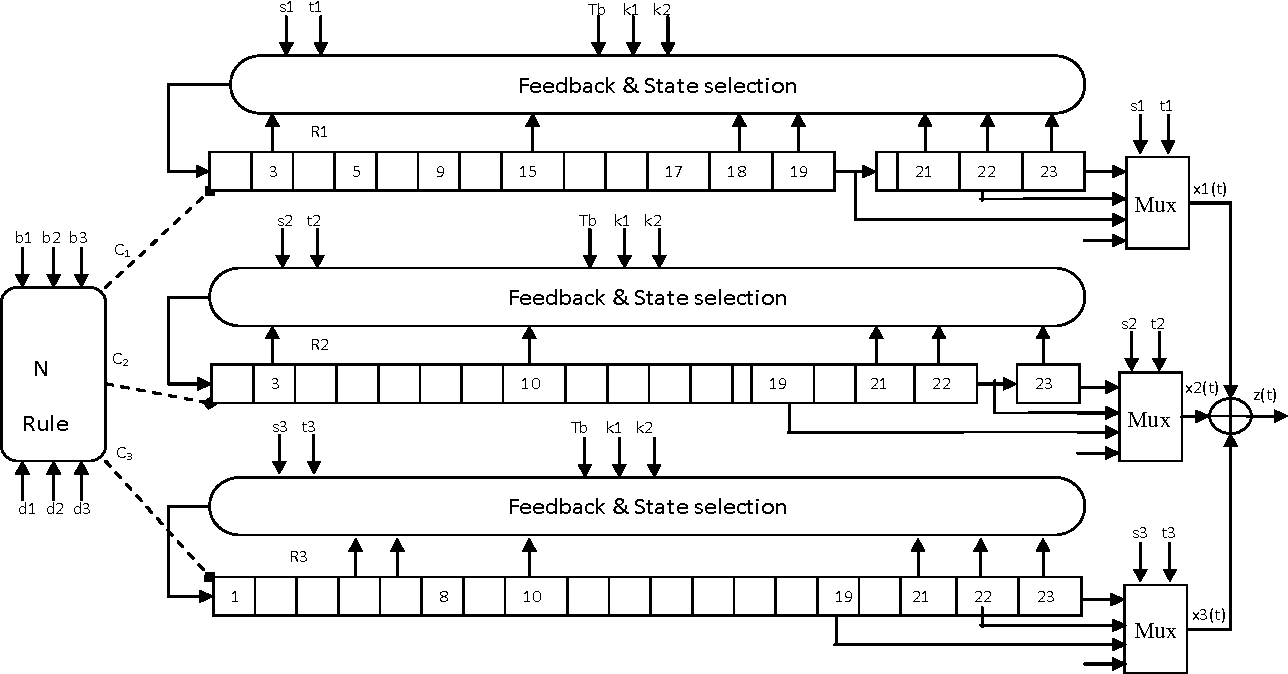
The Reed-Solomon codes with \( n=255 \) are very common, since then each symbol is an element of \( GF(2^8) \) and can be represented as a single byte. They are not binary codes each symbol must have \( 2^m \) possible values, and is typically an element of \( GF(2^m) \). A Reed-Solomon \( (n,k) \) code, where \( n=2^m-1 \) and \( k=n-2t \), can correct up to \( t \) errors. Reed-Solomon codes, like many other error-correcting codes, are parameterized. We’re also going to talk about some performance metrics of error-correcting codes. We’ll see that encoding a message using Reed-Solomon is fairly simple, so easy that we can even do it in C on an embedded system. (I had meant to cover this topic in Part XV, but the article was getting to be too long, so I’ve split it roughly in half.) These are one of the workhorses of error-correction, and they are used in overwhelming abundance to correct short bursts of errors. This time we are going to cover Reed-Solomon codes.

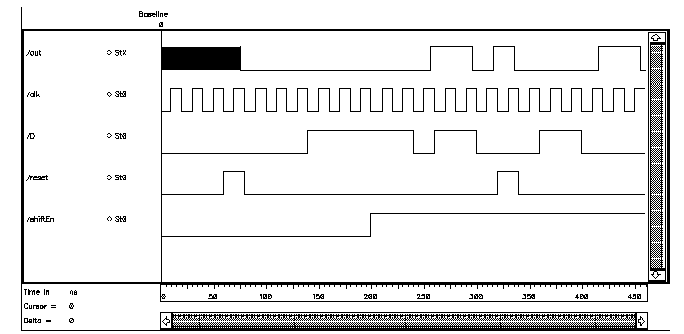
If you are new to this topic, I would strongly suggest going back to read that article before this one. Simple VHDL coding for Galois and Fibonacci LFSR.Last time, we talked about error correction and detection, covering some basics like Hamming distance, CRCs, and Hamming codes.Simple explanation of LFSRs for Engineers.Pseudo-Random Number Generation Routine （ 页面存档备份，存于 互联网档案馆）.(Error detected: period are (2^n)-1 not 2^n) Maximal Length LFSR table （ 页面存档备份，存于 互联网档案馆） with length from 2 to 67.International Telecommunications Union Recommendation O.151 （ 页面存档备份，存于 互联网档案馆） (August 1992).